Heutiger Testraketenstart - Stufe 1c
Kurz weitergecrasht, noch mitnehmen, was geht (auf die Schnelle):
https://sebastiansauer.github.io/crashkurs/
https://sebastiansauer.github.io/crashkurs/
https://sebastiansauer.github.io/crashkurs/
Aha, alles klar. Die mtcars sind übrigens:
Auch hier kann ich bestätigen, dass es so funzt wie angegeben.
https://sebastiansauer.github.io/crashkurs/
Damit bin ich durch, yippieh!!!
Guter Crash-Kurs, werde bestimmt noch mal drauf zurückkommen. Für die Stufe 2 weiß ich jetzt schon genug. Ansonsten habe ich das Meiste schon wieder vergessen - liegt aber an mir, nicht am Kurs, wohlvermerkt!
Bis auf Wiedersehen in Stufe 2, holdorido!!!!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~+
Den erlaube ich mir noch:
Schritt 4: Modellieren
Modellieren hört sich kompliziert an. Für uns hier heißt es vor allem ein inferenzstatistisches Verfahren anzuwenden.
Das Schweizer Taschenmesser unter den Modellierungsverfahren ist die Regressionsanalyse. Man kann sie für viele Zwecke einsetzen.
Wann welchen Test?
Es gibt in vielen Lehrbüchern Übersichten zur Frage, wann man welchen Test rechnen soll. Googeln hilft hier auch weiter. Eine Übersicht findet man hier: http://www.methodenberatung.uzh.ch/de/datenanalyse.html.
https://sebastiansauer.github.io/crashkurs/
Ein bissile Ausprobiererei:
cognitive_biase[1,2] [1] "The tendency to avoid options for which the probability of a favorable outcome is unknown.[10]" > cognitive_biase[1,1:2] Name 1 Ambiguity effect Description 1 The tendency to avoid options for which the probability of a favorable outcome is unknown.[10] > cognitive_biase[11,1:2] Name 11 Bandwagon effect Description 11 The tendency to do (or believe) things because many other people do (or believe) the same. Related to groupthink and herd behavior.[20] > set.seed(100) > x <- rnorm(50, mean = 10, sd = 0.5) > t.test(x, mu=10) One Sample t-test data: x t = 0.70372, df = 49, p-value = 0.4849 alternative hypothesis: true mean is not equal to 10 95 percent confidence interval: 9.924374 10.157135 sample estimates: mean of x 10.04075 > numeric_vector <- c(20, 29, 24, 19, 20, 22, 28, 23, 19, 19) > wilcox.test(numeric_vector, mu=20, conf.int = TRUE) Wilcoxon signed rank test with continuity correction data: numeric_vector V = 30, p-value = 0.1056 alternative hypothesis: true location is not equal to 20 90 percent confidence interval: 19.00006 25.99999 sample estimates: (pseudo)median 23.00002 Warnmeldungen: 1: In wilcox.test.default(numeric_vector, mu = 20, conf.int = TRUE) : gefordertes conf.level nicht erreichbar 2: In wilcox.test.default(numeric_vector, mu = 20, conf.int = TRUE) : kann bei Bindungen keinen exakten p-Wert Berechnen 3: In wilcox.test.default(numeric_vector, mu = 20, conf.int = TRUE) : kann bei Bindungen das exakte Konfidenzinterval nicht berechnen 4: In wilcox.test.default(numeric_vector, mu = 20, conf.int = TRUE) : kann den exakten p-Wert bei Nullen nicht berechnen 5: In wilcox.test.default(numeric_vector, mu = 20, conf.int = TRUE) : kann das exakte Konfidenzinterval bei Nullen nicht berechnen > x <- c(0.80, 0.83, 1.89, 1.04, 1.45, 1.38, 1.91, 1.64, 0.73, 1.46) > y <- c(1.15, 0.88, 0.90, 0.74, 1.21) > wilcox.test(x, y, alternative = "g") # g for greater Wilcoxon rank sum test data: x and y W = 35, p-value = 0.1272 alternative hypothesis: true location shift is greater than 0
Und schon ist die Formatierung wieder im Eimer!
Aus der Tabelle cognitive_biase lässt sich so auswählen:
cognitive_biase[x,y] - grob gesagt.
Mehr dazu hier: 5 Ways to Subset a Data Frame in R | R-bloggers
Und aus der Liste mit den Tests, http://r-statistics.co/Statistical-Tests-in-R.html, habe ich drei ausgewählt (Ergebnisse waren grade oben zu sehen).
Und nun zum Schweizer Taschenmesser, der Regression:
lm(mpg ~ cyl, data = mtcars) Call:
lm(formula = mpg ~ cyl, data = mtcars)
Coefficients:
(Intercept) cyl
37.885 -2.876 lmheißt “lineares Modell” - weil man bei der (normalen) Regression eine Gerade in die Punktewolke der Daten legt, um den Trend zu abzuschätzen. Als nächstes gibt man die “Ziel-Variable” (Output) an, hiermpg. Dann kommt ein Kringel~gefolgt von einer (mehr) Input-Variablen (Prädiktoren, UVs). Schließnoch muss noch die Datentabelle erwähnt werden.
Das Ergbebnis sagt uns, dass pro Zylinder die Variablempgum knapp 3 Punkte sinkt. Also: Hat die Karre einen Zylinder mehr, so kann man pro Galone Sprit 3 Meilen weniger fahren. Immer im Schnitt, versteht sich. (Und wenn die Voraussetzungen erfüllt sind, aber darum kümmern wir uns jetzt nicht.)
https://sebastiansauer.github.io/crashkurs/
Man kann auch mehrere Prädiktoren anführen:
lm(mpg ~ cyl + hp, data = mtcars) Call: lm(formula = mpg ~ cyl + hp, data = mtcars) Coefficients: (Intercept) cyl hp 36.90833 -2.26469 -0.01912
Dazu werden die durch + getrennt. Die Ergebnisse zeigen uns, dass die PS-Zahl (´hp´) kaum Einfluss auf den Spritverbrauch haut. Genauer: Kaum zusätzlichen
Einfluss auf den Spritverbrauch hat. Also Einfluss, der über den
Einfluss hinausgeht, der schon durch die Anzahl der Zylinder erklärt
werden würde. Es ist also praktisch wurscht, wie viel PS das Auto hat,
wenn man den Verbrauch schätzen will - Hauptsache, man weiß die Anzahl
der Zylinder.
https://sebastiansauer.github.io/crashkurs/
Aha, alles klar. Die mtcars sind übrigens:
mtcars mpg cyl disp hp drat wt qsec vs am gear carb Spass Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 FALSE Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 FALSE Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 FALSE Hornet 4 Drive 21.4 6 258.0 110 3.08 3.215 19.44 1 0 3 1 FALSE Hornet Sportabout 18.7 8 360.0 175 3.15 3.440 17.02 0 0 3 2 FALSE Valiant 18.1 6 225.0 105 2.76 3.460 20.22 1 0 3 1 FALSE Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4 TRUE Merc 240D 24.4 4 146.7 62 3.69 3.190 20.00 1 0 4 2 FALSE Merc 230 22.8 4 140.8 95 3.92 3.150 22.90 1 0 4 2 FALSE Merc 280 19.2 6 167.6 123 3.92 3.440 18.30 1 0 4 4 FALSE Merc 280C 17.8 6 167.6 123 3.92 3.440 18.90 1 0 4 4 FALSE Merc 450SE 16.4 8 275.8 180 3.07 4.070 17.40 0 0 3 3 FALSE Merc 450SL 17.3 8 275.8 180 3.07 3.730 17.60 0 0 3 3 FALSE Merc 450SLC 15.2 8 275.8 180 3.07 3.780 18.00 0 0 3 3 FALSE Cadillac Fleetwood 10.4 8 472.0 205 2.93 5.250 17.98 0 0 3 4 TRUE Lincoln Continental 10.4 8 460.0 215 3.00 5.424 17.82 0 0 3 4 TRUE Chrysler Imperial 14.7 8 440.0 230 3.23 5.345 17.42 0 0 3 4 TRUE Fiat 128 32.4 4 78.7 66 4.08 2.200 19.47 1 1 4 1 FALSE Honda Civic 30.4 4 75.7 52 4.93 1.615 18.52 1 1 4 2 FALSE Toyota Corolla 33.9 4 71.1 65 4.22 1.835 19.90 1 1 4 1 FALSE Toyota Corona 21.5 4 120.1 97 3.70 2.465 20.01 1 0 3 1 FALSE Dodge Challenger 15.5 8 318.0 150 2.76 3.520 16.87 0 0 3 2 FALSE AMC Javelin 15.2 8 304.0 150 3.15 3.435 17.30 0 0 3 2 FALSE Camaro Z28 13.3 8 350.0 245 3.73 3.840 15.41 0 0 3 4 TRUE Pontiac Firebird 19.2 8 400.0 175 3.08 3.845 17.05 0 0 3 2 FALSE Fiat X1-9 27.3 4 79.0 66 4.08 1.935 18.90 1 1 4 1 FALSE Porsche 914-2 26.0 4 120.3 91 4.43 2.140 16.70 0 1 5 2 FALSE Lotus Europa 30.4 4 95.1 113 3.77 1.513 16.90 1 1 5 2 FALSE Ford Pantera L 15.8 8 351.0 264 4.22 3.170 14.50 0 1 5 4 TRUE Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6 FALSE Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8 TRUE Volvo 142E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2 FALSE
A data frame with 32 observations on 11 (numeric) variables.
| [, 1] | mpg | Miles/(US) gallon |
| [, 2] | cyl | Number of cylinders |
| [, 3] | disp | Displacement (cu.in.) |
| [, 4] | hp | Gross horsepower |
| [, 5] | drat | Rear axle ratio |
| [, 6] | wt | Weight (1000 lbs) |
| [, 7] | qsec | 1/4 mile time |
| [, 8] | vs | Engine (0 = V-shaped, 1 = straight) |
| [, 9] | am | Transmission (0 = automatic, 1 = manual) |
| [,10] | gear | Number of forward gears |
| [,11] | carb | Number of carburetors |
lm(mpg ~ cyl + wt, data = mtcars) Call: lm(formula = mpg ~ cyl + wt, data = mtcars) Coefficients: (Intercept) cyl wt 39.686 -1.508 -3.191Scheint sich zu bestätigen.
Vorhersagen
Man kann die Regression nutzen, um Vorhersagen zu treffen. Sagen wir, unser neuer Lamborghini hat 400 PS und 12 Zylinder. Wie groß ist wohl der Spritverbrauch laut unserem Regressionsmodell?
Als Vorbereitung speichern wir unser Regressionsmodell in einer eigenen Variablen:
mein_lm <- lm(mpg ~ cyl + hp, data = mtcars)
Dazu nimmt man am besten den Befehl predict, weil wir wollen eine Vorhersage treffen:
predict(mein_lm, data.frame(cyl = 12, hp = 400)) 1 2.083329
Aha. Pro Gallone kämmen wir 2 Meilen. Schluckspecht.
https://sebastiansauer.github.io/crashkurs/Visualisierung des Modells
Schauen wir uns das Modell mal an, damit es nicht so theoretisch ist. Wie gesagt, ein Regressionsmodell ist nichts anderes als eine Trendgerade in einer Punktewolke.
Gerade sind durch Achsenabschnitt (engl. “intercept”) f(x=0) und Steigung (englisch: “slope”) definiert. Der Steigungswert ist die Zahl, die der lm-Befehl für den Prädiktor ausspuckt
qplot(x = cyl, y = mpg, data = mtcars, geom = "point") + geom_abline(slope = -2.9, intercept = 38)
Auch hier kann ich bestätigen, dass es so funzt wie angegeben.
Schritt 5: Kommunizieren
Kommunizieren soll sagen, dass Sie Ihre Ergebnisse anderen mitteilen - als Student heißt das häufig in Form einer Seminararbeit an den Dozenten.
Einige Hinweise:
- Geben Sie nicht alle Ergebnisse heraus. Ihre Fehler müssen niemanden interessieren.
- Die wesentlichen Ergebnisse kommen in den Hauptteil der Arbeit. Interessante Details in den Anhang.
- Der Mensch ist ein Augentier. Ihr Gutachter auch. Achten Sie auf optisch ansprechende Darstellung; schöne Diagramme helfen.
- Dozenten achten gerne auf formale Korrektheit. Das Gute ist, dass dies relativ einfach sicherzustellen ist, da auf starren Regeln basierend.
Tabellen und Diagramme
Daten kommunizieren heißt praktisch zumeist, Tabellen oder Diagramme zu erstellen. Meist gibt es dazu Richtlinien von Seiten irgendeiner (selbsterannten) Autorität wie Dozenten oder Fachgesellschaften. Zum Beispiel hat die APA ein umfangreiches Manual zum Thema Manuskripterstellung publiziert; die deutsche Fachgesellschaft der Psychologie entsprechend. Googeln Sie mal, wie in ihren Richtlinien Tabellen und Diagramme zu erstellen sind (oder fragen Sie Ihren Gutachter).
Für Fortgeschrittene: RMarkdown
Wäre das nicht cool: Jegliches Formatieren wird automatisch übernommen und sogar so, das ses schick aussieht? Außerdem wird Ihr R-Code und dessen Ergebnisse (Tabellen und Diagramme oder reine Zahlen) automatisch in Ihr Dokument übernommen. Keine Copy-Paste-Fehler mehr. Keine händisches Aktualisieren, weil Sie Daten oder die vorhergehende Analyse geändert haben. Hört sich gut an? Probieren Sie mal RMarkdown aus :one_up:.
Fazit
Glück auf
Hier finden Sie einen Überblick an einige “Lieblings-R-Befehle”.
https://sebastiansauer.github.io/crashkurs/
Damit bin ich durch, yippieh!!!
Guter Crash-Kurs, werde bestimmt noch mal drauf zurückkommen. Für die Stufe 2 weiß ich jetzt schon genug. Ansonsten habe ich das Meiste schon wieder vergessen - liegt aber an mir, nicht am Kurs, wohlvermerkt!
Bis auf Wiedersehen in Stufe 2, holdorido!!!!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~+
Den erlaube ich mir noch:
qplot(x = wt + cyl, + y = mpg, + data = mtcars, + geom = "point") + + geom_abline(slope = -2.9, intercept = 38)
Wer aufgepasst hat, weiß Bescheid.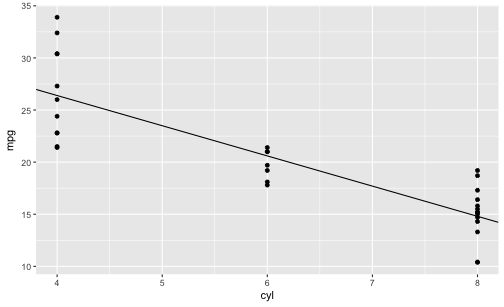


Kommentare
Kommentar veröffentlichen